In a recent post I wrote about a fretboard insight that came to me as I was revisiting the well-known CAGED system. Here I’d like to offer an alternate presentation of the same insight. So what is it, exactly? I think of it as a way of generalizing CAGED beyond five positions, to cover any position on the fretboard.
We are going to explore the concept in three simple steps:
- Review the fingerings for all twelve major keys in open position.
- Convert each of these twelve open-position fingerings into a movable pattern.
- Play a scale of our choice, say E major, in twelve different positions on the fretboard. Starting in open position, we’ll move up fret by fret, using each pattern once in a logical order.
Step 1 is straightforward. The diagram below shows an open-position fingering for each of the twelve major keys. The strategy used in these fingerings is to choose an open string wherever possible, never fretting a note that’s available open.
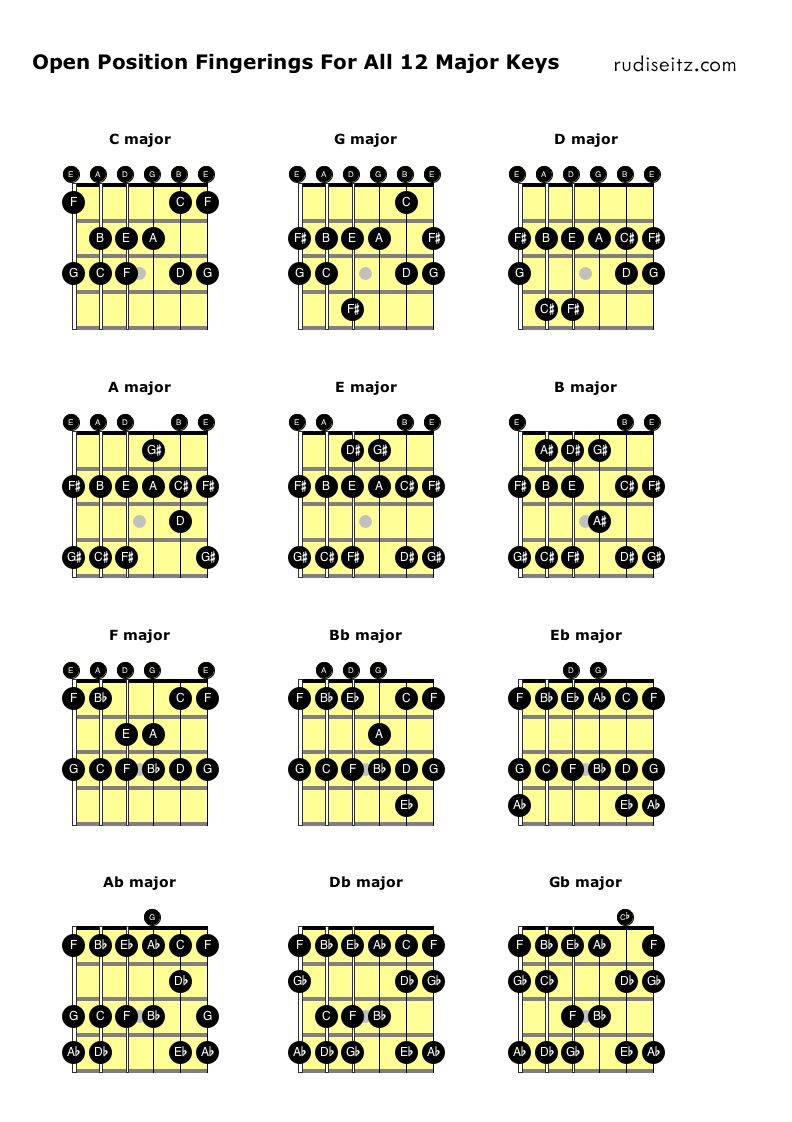
Now for Step 2, we’ll take each of the above fingerings and convert it into a movable pattern. We’ll do this by shifting the pattern up to an arbitrary place on the fretboard and fretting any notes that were open.
Of course, as we move the pattern around the fretboard, it will produce different notes, but we’ll always call it by the name of its open-position key. For example, there will be a “C pattern” that we derive from the fingering of the C major scale in open position. We’ll continue to call this pattern the “C pattern” no matter where we use it on the fretboard. If we use it to play a D major scale at the second fret, we’ll say that we’re “playing a D major scale with the C pattern.”
The diagram below shows twelve movable patterns derived from the open-position fingerings above. Unlike the fingerings above, these patterns aren’t specific to any position: they can be played anywhere on the fretboard.
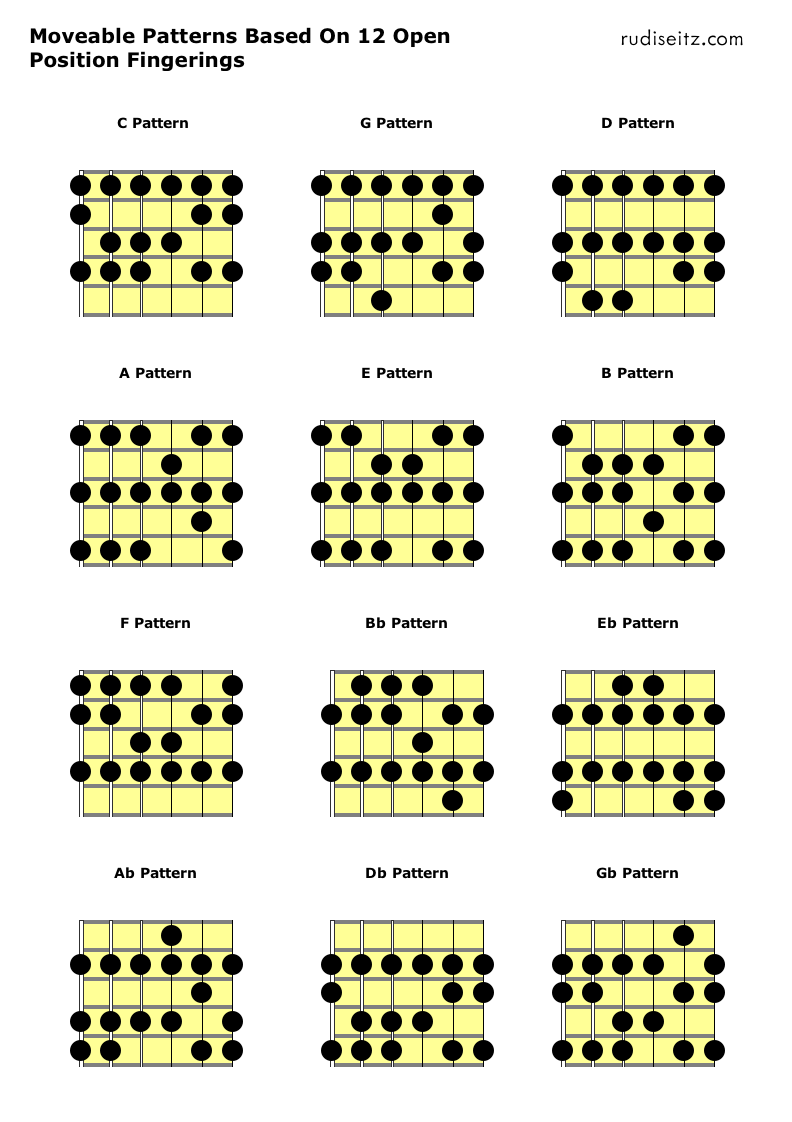Before we continue, let’s make one important observation about these movable patterns. As noted above, any given pattern will generate the notes of a different key as we shift it up the fretboard. The C pattern produces C major in open position, C# major at the first fret, D major at the second fret, and so on. However, the intervallic relationship between any two patterns is constant when you play them both at the same fret. For example, the C pattern and the G pattern have roots that are a perfect fifth apart. Obviously, if I play the C pattern in open position and then I play the G pattern in open position, I’ve moved the key up a fifth. This relationship holds true at any fret. If I’m playing the C pattern at the fourth fret, I don’t even need to think about what key I’m actually playing in (it’s E, but that doesn’t matter), I can switch to the key a fifth above just by switching to the G pattern at the fourth fret (now I’ll be in B, but I don’t need to know that).
In Step 3, we’ll now see how we can play an E major scale anywhere on the fretboard, using the twelve movable patterns that we’ve just considered.
The diagram below shows that to play an E major scale in open position we can use the E pattern (of course); to play an E major scale in first position we can use the Eb pattern (that’s a little more interesting); to play an E major scale in second position we can use the D pattern.
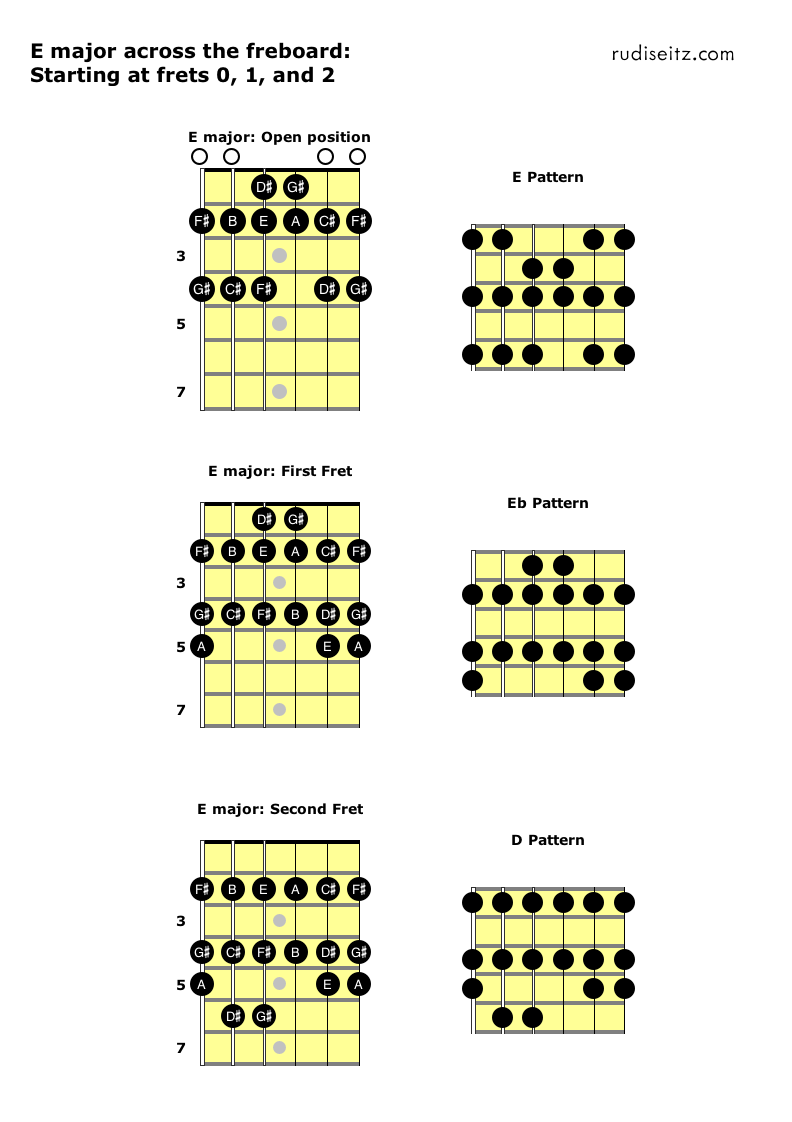Before we move on, let’s take a moment to understand what’s happening here. Each time we move up a fret, the appropriate pattern’s name shifts down a semitone. As we move from open position, to first position, to second position, we use the E pattern, then the Eb pattern, then the D pattern. Why do the pattern names descend like that as the position ascends?
Here’s a way to think of it. If you’re playing E major in open position and you shift the whole fingering pattern up a fret, you will have raised every note by a half-step, putting you in F major. In order to return to E, you’d need to find a way of lowering everything a half-step while staying in your new position. You can do this by changing from the E pattern to the Eb pattern in that same position: those two patterns have a half-step root relationship.
Now say you’re at the first fret, playing the Eb pattern to generate the notes of E major, and you decide to move up another fret. At the second fret, the Eb pattern will generate F, so if you want to stay in E major, you’ll need to compensate again. Again, you’ll need to play the pattern that’s rooted a half-step lower – you’ll want the D pattern here.
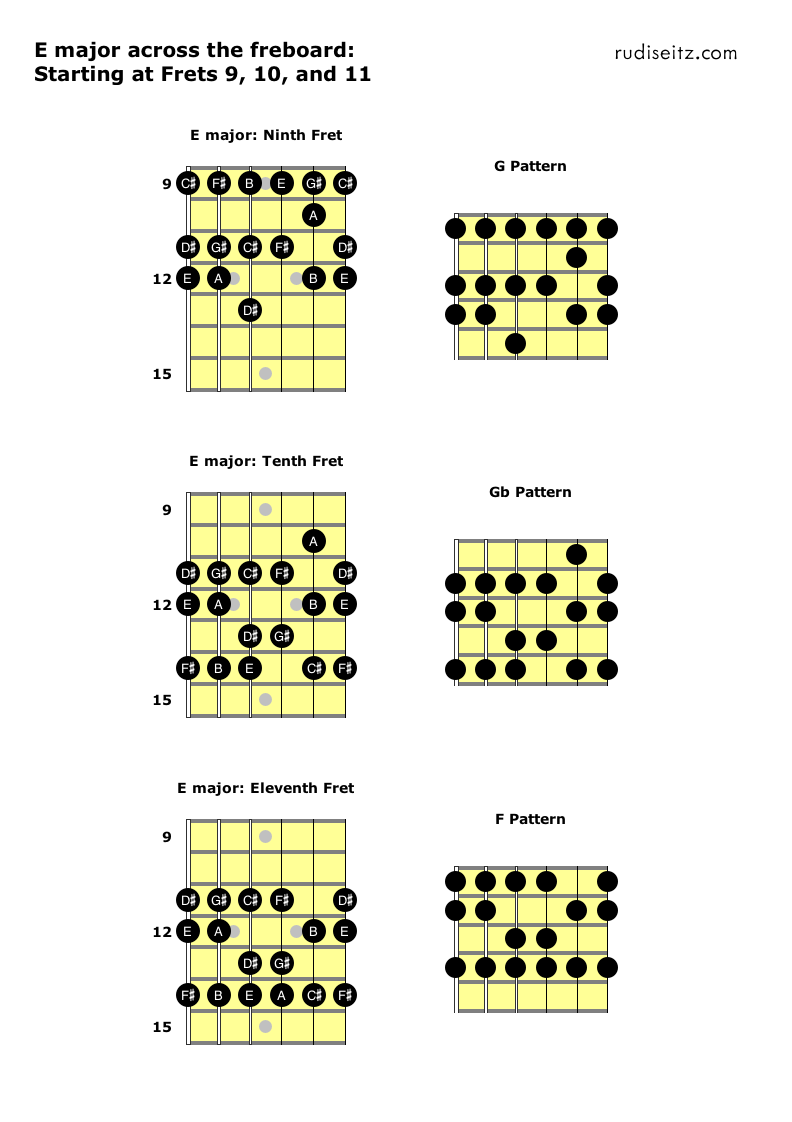
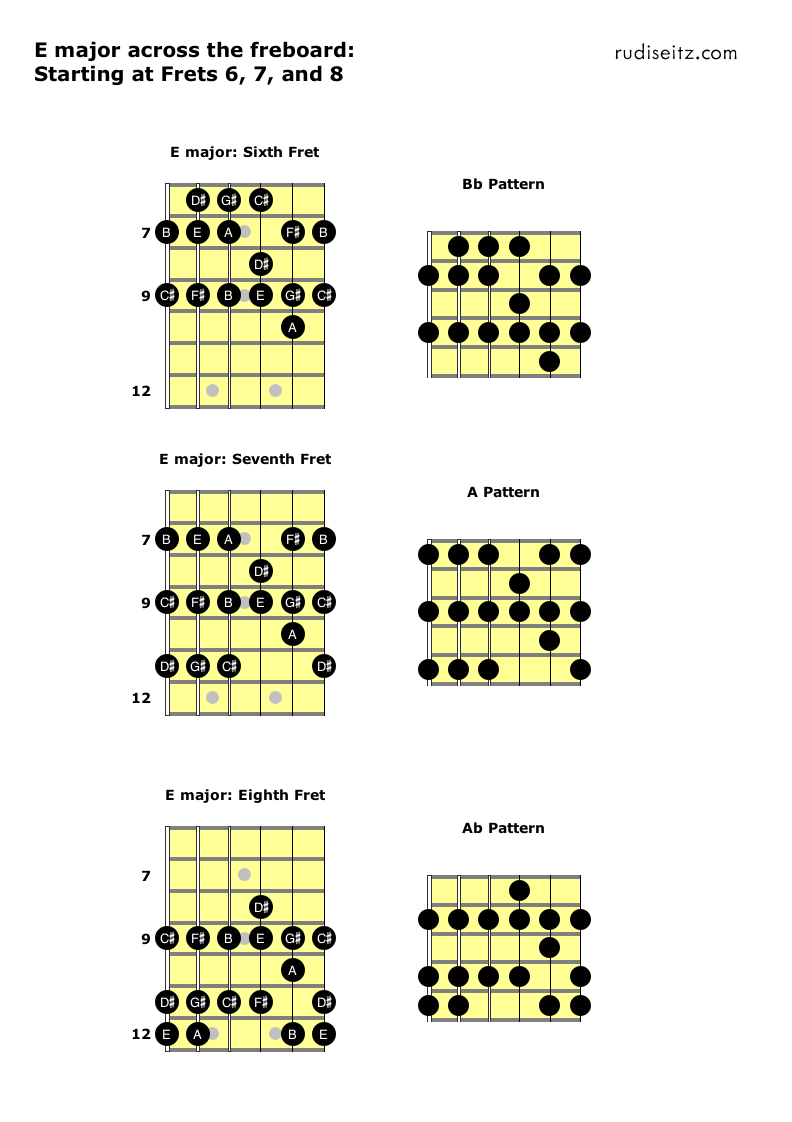
The next diagram shows how we can use the Db, C, and B patterns as we shift up to frets 3, 4, and 5.
Notice that the Db pattern is inconvenient, since no notes fall under the index finger. We might as well just move the index finger up a fret and think of the pattern as being the C pattern. Nevertheless, we show the Db pattern here so that all patterns and positions are accounted for.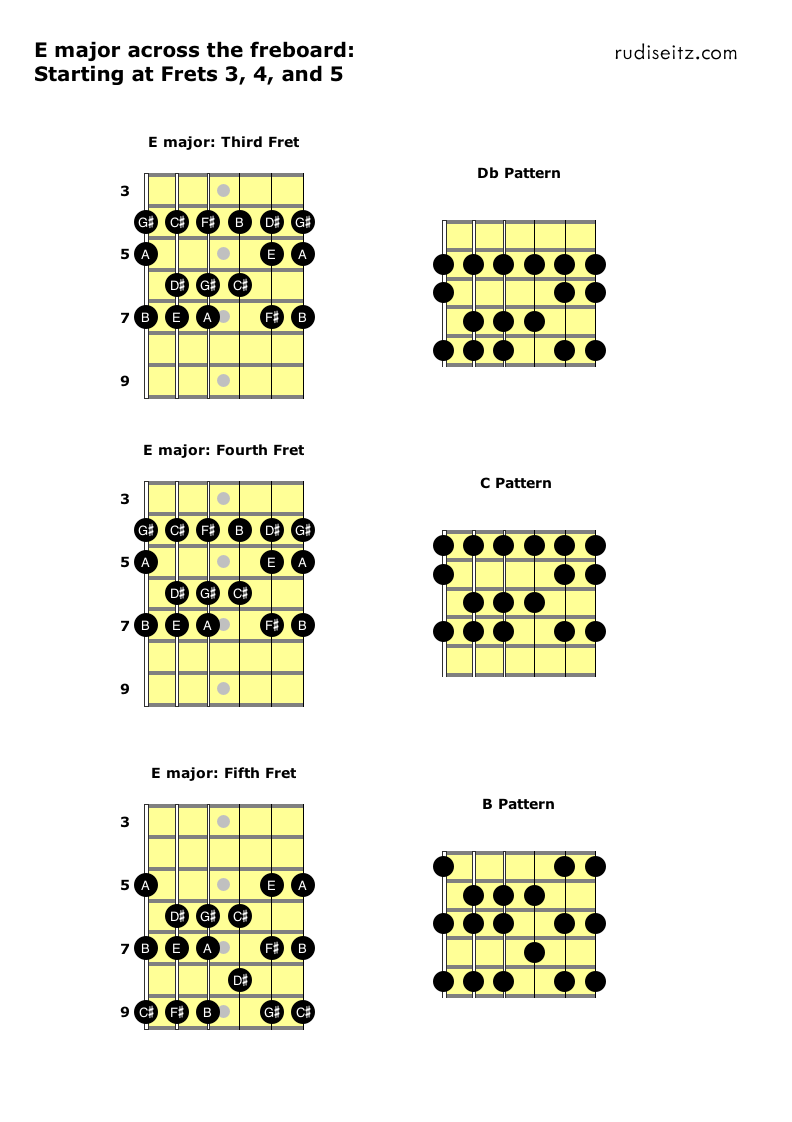
The next two diagrams show the rest of the possible positions and the patterns that give E major at each of those positions:
Now let’s summarize what we’ve seen.
Most presentations of CAGED go something like this: Take the familiar open-position chords – C, A, G, E, D – and turn them into movable barre chords. Then learn a major (or other) scale pattern that fits over each shape. Then notice how you can play in a given key all over the fretboard by placing these chord shapes at appropriate positions and playing the corresponding scale patterns over the shapes.
We’ve taken a different approach. We’ve derived movable major-scale patterns from the open-position fingerings for each of the twelve keys. Then we’ve noticed how these movable patterns let us continue playing in the same key as we shift our left hand up the neck, fret by fret: each time we go a fret higher we switch to the pattern that’s named a semitone lower.
Moving our left hand up a fret transposes everything a semitone higher; switching from pattern X to pattern X-flat transposes everything a semitone lower. The transpositions cancel out and we stay in the same key. It’s sort of obvious and sort of magical, I think. ■