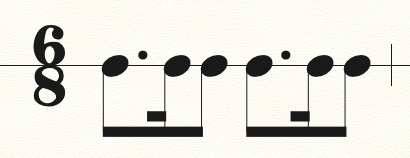
In working on my latest composition, I happened to sketch a repeating eighth-sixteenth-eighth rhythm, like this:
Noticing how simple this rhythm looked on the page and how familiar it sounded, I didn’t expect that it would trigger a fit of soul-searching.
But two questions soon arose: first, did I mean to write this exact rhythm, or had I been thinking of a dotted rhythm in 6/8 – had I just forgotten to include the dots? Perhaps I had been aiming for this:
Second, if the original rhythm without the dots is what I really wanted, then what time signature did it belong in? If you take a dotted rhythm in 6/8 and remove the dots without making any other adjustments, what are you left with and how should you notate it?
The dotless rhythm has a total of five eighth notes as opposed to the six that we get when we include the dots. I’ll leave it as an exercise for the reader to discover the chaos that ensues when you try to express a quintuple pattern in a duple, triple, or quadruple meter. Suffice it to say that 6/8, 4/4, and other “go-to” time signatures are not suitable homes for this particular rhythm. Now, 5/8 might come to mind as the proper choice, but 5/8 would typically imply a grouping of the eighths as 3+2 or 2+3. In our case, the grouping is 2.5+2.5.
We could still use 5/8 if we double the note values and spread one of our original measures across two measures, like this:
That looks nice and clean to me. The downside is that each group of three notes now has its own measure and we lose the hierarchy of a stronger and a weaker group within the same measure. And perhaps this is an artificial concern, but the 5/8 notation with the long note values looks quite different from the 6/8 that we’re comparing it with. I’d like to keep them looking similar on the page if possible, so the dots come into focus as the thing that we’re varying.
Another option is to count in sixteenths instead of eighths. We can use a time signature of 10/16 with a grouping of the sixteenths as (3+2)+(3+2) as shown below. For better or worse, this is the option that I’ll be using:
Now back to the first question: what’s the qualitative difference between this 10/16 rhythm and the common dotted rhythm in 6/8? What do the dots “do” for us aside from helping us achieve an even number of beats in the measure? What happens aesthetically when we take them out? Is there a compelling reason to choose the 10/16 over the 6/8 or are they similar enough that we’d be better off using the much more familiar 6/8 option and letting the performer vary the feel as appropriate? Could the 10/16 be considered a performance variation of the 6/8? Is it a representation of a how a performer might interpret the 6/8 if, instead of applying the practice of “overdotting,” they applied “underdotting” – or is it something more distinctive? – something that isn’t comparable to 6/8 at all?
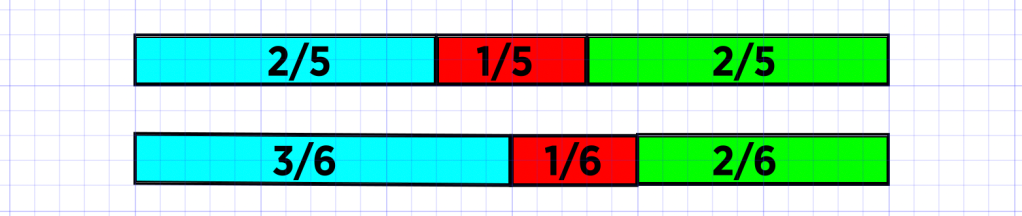
When you take the dots out, of course, you’re affecting more than the notes that had the dots – you’re affecting the ratios between those notes and all the other ones. The first three durations of our dotless rhythm are in a 2:1:2 ratio, while the first three durations of the dotted 6/8 rhythm are in a 3:1:2 ratio. (Ignore the second three durations for now because they follow the same pattern.) So the question we’re really asking is: What’s the musical difference between 2:1:2 and 3:1:2? To make a visual comparison of these ratios, we’d want to view them as alternate ways of subdividing the same distance on the page. If we take a portion of graph paper that’s 30 cells long, the 2:1:2 ratio could be expressed as 12 + 6 + 12 cells and the 3:1:2 ratio could be expressed as 15 + 5 + 10 cells, as shown below. (Note that the labels in the image – 2/5, 1/5, etc. – are fractions, not time signatures.)
Our graph shows what happens when we normalize the ratios/rhythms to occupy the same total distance/duration. Reading left to right, we see that the second (red) and third (green) hits in the dotless rhythm on top come earlier than the second and third hits in the dotted rhythm below – which should be no surprise – but now we can see how much earlier. The second hit is 3 cells earlier while the third hit is 2 cells earlier. What does a cell represent? If we like, we could map each cell to a sixteenth note and then our graph would represent a single bar in the time signature 30/16 – that’s the level of resolution we’d need if we want to express the two ratios in a way where they both fill the same measure.
But let’s get back to our original 6/8 and 10/16 rhythms. How do they sound? To get a sense for their similarities and differences, it would be helpful to hear the two rhythms in sequence, one after the other. If we do this in a way where the tempo stays fixed, the 6/8 will sound slower because it has an extra eighth. That slowdown will get in the way of our comparison because, of course, neither rhythm is inherently slower or faster than the other – it depends on how we play them. To make a comparison that’s not biased by speed, we’d like one bar of the 6/8 to take the same time as one bar of the 10/16, just as our graph above stretches the 2:1:2 and 3:1:2 ratios across a common span of 30 cells. If the six beats from a 6/8 bar have to fit in the space of five, that means the tempo has to be multiplied by 6/5 or 1.2. So if we play a 10/16 measure at 100 quarters-per-minute (QPM), we have to play a 6/8 measure at 120 QPM for it to take the same time. Here’s how we can perform the two rhythms in a way where the measure duration stays fixed:
In this clip, you can hear exactly what’s shown above; following that, you’ll hear an extended section of the 10/16 rhythm, then a pause, and then an extended section of the 6/8.
How do the two rhythms compare when melody is involved? Below, I’ve provided a melodic fragment set first to the 10/16 rhythm and then to the 6/8. Note that each clip contains two statements of the melody (with a transposition) but the notation only shows one statement.
The 10/16 Version
The 6/8 Version
How do these two renderings of the melody strike you? I’m impressed by how similar they are at a high level, but how different they are in many subtle ways. The tune seems to carry the same meaning in each case, but the feel is different. For me, the 10/16 feels like a swift walk, while the 6/8 is more of a skip or gallop, more dance-like. The 10/16 has less emphasis on the first beat of each group. There’s less differentiation overall because only two rhythmic values are used (8th and 16th) as opposed to three (dotted-8th, 8th, and 16th). I also hear more of a backbeat. The 6/8 establishes more of a hierarchy among the hits. The first beat of each group stands out more clearly as a landing point, as we’d expect because it’s the longest. The rhythm sounds more smooth and stable overall, with less funk – each hit seems to occupy its own designated place in the measure, with no ambiguity. The 6/8 is a fully “settled” rhythm as opposed to the 10/16 which seems slightly unstable. All of that said, if I weren’t paying close attention, it’s conceivable that I’d mistake one rhythm for the other, or at least consider them as two interpretations of the same underlying thing.
Want to hear the two versions played simultaneously? I could superimpose the audio clips from above, but instead I’ll make a new clip based on the following notation where the 6/8 measures have been jammed into the 10/16 measures using tuplets. The 6/8 version is in the treble clef while the 10/16 version is in the bass.
I’d say that all the subtle aesthetic differences between the two versions are obscured when we superimpose them, and we’re left with something that sounds like… what a performer might actually play, if they were playing very loosely, with the left and right hands a little bit staggered.
Just for fun, here’s how it sounds at an extremely slow 20 QPM:
What can we conclude from all of this? When you take a dotted 6/8 rhythm and remove the dots on the eighth notes without adjusting the corresponding sixteenths, you’re left with a quintuple rhythm that you could express in 5/8 with doubled note values, or in 10/16 using equivalent note values. To accurately compare the two rhythms, you’ve got to adjust the tempo so the duration of a measure stays fixed. The new rhythm could sound like a variation of 6/8, or like something totally different, depending on your ear and on the context: the melodic material at play, the overall tempo, the level of rhythmic precision you’re performing with, and so on. This is subjective but I’d say the 6/8 is more dance-like, with more clarity and stability while the 10/16 is more like a brisk walk with more funk and internal ambiguity.
So what decision did I make in the end? Well, it turned out that I needed to use 10/16 because I was doing something weird. I was writing a retrograde canon where the theme was being superimposed on a backwards version of itself. When you do that, some pairs of notes from the forwards and backwards themes fall into alignment on a shared beat; but these alignments work out differently depending on whether you’re in 10/16 or 6/8. I wanted the 10/16 alignments. If the context had been simpler, then it might have been a harder choice, and I would have felt more pressure to go with the more standard option. But this brings up an important point: when comparing two rhythms, you’ve got to do more than listen to them side-by-side. You’ve got to consider how they might interact with counter-rhythms of different sorts – and that’s an open-ended question.
If you’d like to hear where I used the 10/16 rhythm in my latest piece, check out Ammolite and go to 7:05 in the audio clip. ■